傅里叶变换
# 思维导图
# 理论基础
图像处理一般分为空间域处理和频率域处理。
空间域处理是直接对图像内的像素进行处理。
频率域处理是先将图像变换到频率域,然后在频率域对图像进行处理,最后通过反变换将图像从频率域变换到空间域。傅里叶变换是应用最广泛的一种频域变换,它能够将图像从空间域变换到频率域,而逆傅里叶变换能够将频率信息变换到空间域内。
傅里叶变换的目的,就是为了将图像从空域转换到频域,并在频域内实现对图像内特定对象的处理,然后再对经过处理的频域图像进行逆傅里叶变换得到空域图像。傅里叶变换在图像处理领域发挥着非常关键的作用,可以实现图像增强、图像去噪、边缘检测、特征提取、图像压缩和加密等。
# Numpy实现傅里叶变换
Numpy模块提供了傅里叶变换功能,Numpy模块中的fft2()函数可以实现图像的傅里叶变换。
# 1.实现傅里叶变换
Numpy提供的实现傅里叶变换的函数是numpy.fft.fft2(),它的语法格式是:
返回值 = numpy.fft.fft2(原始图像)
- 参数“原始图像”的类型是灰度图像
- 函数的返回值是一个复数数组(complex ndarray)。
经过该函数的处理,就能得到图像的频谱信息。此时,图像频谱中的零频率分量位于频谱图像(频域图像)[插图]的左上角,为了便于观察,通常会使用numpy.fft.fftshift()函数将零频率成分移动到频域图像的中心位置
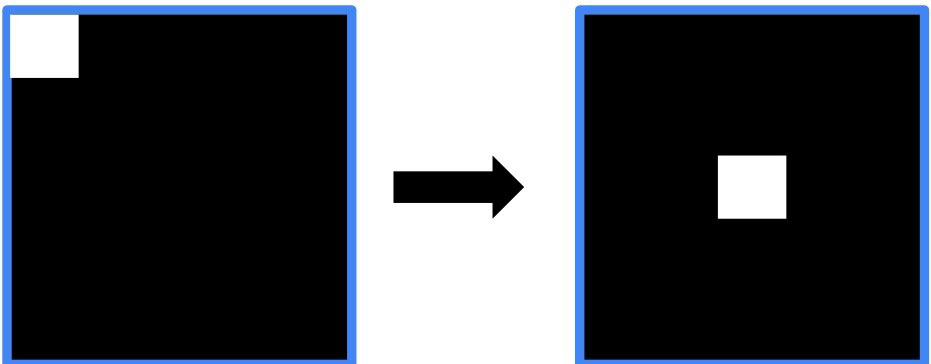
函数numpy.fft.fftshift()的语法格式是:
返回值=numpy.fft.fftshift(原始频谱)
使用该函数处理后,图像频谱中的零频率分量会被移到频域图像的中心位置,对于观察傅里叶变换后频谱中的零频率部分非常有效。
对图像进行傅里叶变换后,得到的是一个复数数组。为了显示为图像,需要将它们的值调整到[0, 255]的灰度空间内,使用的公式为:
像素新值=20*np.log(np.abs(频谱值))
实例一:用Numpy实现傅里叶变换,观察得到的频谱图像。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('image\\lena.bmp',0)
# 傅里叶变换
f = np.fft.fft2(img)
# 将低频移动到中间
fshift = np.fft.fftshift(f)
# 将复数数组调整到灰度空间内
magnitude_spectrum = 20*np.log(np.abs(fshift))
# 显示原始图像
plt.subplot(121)
plt.imshow(img, cmap = 'gray')
plt.title('original')
plt.axis('off')
plt.subplot(122)
# 显示频谱图
plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('result')
plt.axis('off')
plt.show()

# 2.实现逆傅里叶变换
1.如果在傅里叶变换过程移动了零频率分量,逆变换过程需要通过numpy.fft.ifftshift()函数将零频率分量移到原来的位置。
2.进行逆傅里叶变换
函数numpy.fft.ifftshift()是numpy.fft.fftshift()的逆函数,其语法格式为:
调整后的频谱 = numpy.fft.ifftshift(原始频谱)
numpy.fft.ifft2()函数可以实现逆傅里叶变换,返回空域复数数组。
返回值=numpy.fft.ifft2(频域数据)
函数numpy.fft.ifft2()的返回值仍旧是一个复数数组(complex ndarray)。
逆傅里叶变换得到的空域信息是一个复数数组,需要将该信息调整至[0, 255]灰度空间内,使用的公式为:
iimg = np.abs(逆傅里叶变换结果)
实例二:在Numpy内实现傅里叶变换、逆傅里叶变换,观察逆傅里叶变换的结果图像。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('image\\boat.bmp',0)
# 傅里叶变换
f = np.fft.fft2(img)
# 移动零点位置
fshift = np.fft.fftshift(f)
# 还原零点位置
ishift = np.fft.ifftshift(fshift)
# 逆傅里叶变换
iimg = np.fft.ifft2(ishift)
# 还原图像
iimg = np.abs(iimg)
# 打印图像
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122), plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'), plt.axis('off')
plt.show()

# 3.高通滤波示例
在一幅图像内,同时存在着高频信号和低频信号。
- 低频信号对应图像内变化缓慢的灰度分量。例如,在一幅大草原的图像中,低频信号对应着颜色趋于一致的广袤草原。
- 高频信号对应图像内变化越来越快的灰度分量,是由灰度的尖锐过渡造成的。如果在上面的大草原图像中还有一头狮子,那么高频信号就对应着狮子的边缘等信息。
滤波器能够允许一定频率的分量通过或者拒绝其通过,按照其作用方式可以划分为低通滤波器和高通滤波器。
- 允许低频信号通过的滤波器称为低通滤波器。低通滤波器使高频信号衰减而对低频信号放行,会使图像变模糊。
- 允许高频信号通过的滤波器称为高通滤波器。高通滤波器使低频信号衰减而让高频信号通过,将增强图像中尖锐的细节,但是会导致图像的对比度降低。
傅里叶变换可以将图像的高频信号和低频信号分离
高通滤波实现:将傅里叶变换结果图像result中的低频分量值都替换为0(处理为黑色),就屏蔽了低频信号,只保留高频信号,实现高通滤波。
需要先计算其中心位置的坐标,然后选取以该坐标为中心,上下左右各30个像素大小的区域,将这个区域内的像素值置零。该滤波器的实现方法为:
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0

实例三:在Numpy内对图像进行傅里叶变换,得到其频域图像。然后,在频域内将低频分量的值处理为0,实现高通滤波。最后,对图像进行逆傅里叶变换,得到恢复的原始图像。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('image\\boat.bmp',0)
# 傅里叶变换
f = np.fft.fft2(img)
# 将零频域移动到中间
fshift = np.fft.fftshift(f)
# 构建低频区域
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
# 将频谱中间置零
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
# 将零频域还原
ishift = np.fft.ifftshift(fshift)
# 逆傅里叶变换
iimg = np.fft.ifft2(ishift)
# 得到图像
iimg = np.abs(iimg)
# 显示图像
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122), plt.imshow(iimg, cmap = 'gray')
plt.title('iimg'), plt.axis('off')
plt.show()

# OpenCV实现傅里叶变换
OpenCV提供了函数cv2.dft()和cv2.idft()来实现傅里叶变换和逆傅里叶变换
# 1.实现傅里叶变换
函数cv2.dft()的语法格式为:
返回结果=cv2.dft(原始图像,转换标识)
- 对于参数“原始图像”,要首先使用np.float32()函数将图像转换成np.float32格式。
- “转换标识”的值通常为“cv2.DFT_COMPLEX_OUTPUT”,用来输出一个复数阵列。
函数cv2.dft()返回的结果与使用Numpy进行傅里叶变换得到的结果是一致的,但是它返回的值是双通道的,第1个通道是结果的实数部分,第2个通道是结果的虚数部分。
经过函数cv2.dft()的变换后,我们得到了原始图像的频谱信息。此时,零频率分量并不在中心位置,为了处理方便需要将其移至中心位置,可以用函数numpy.fft.fftshift()实现。
dftShift = np.fft.fftshift(dft)
经过上述处理后,频谱图像还只是一个由实部和虚部构成的值。要将其显示出来,还要做进一步的处理才行。函数cv2.magnitude()可以计算频谱信息的幅度。
返回值=cv2.magnitude(参数1,参数2)
- 参数1:浮点型x坐标值,也就是实部。
- 参数2:浮点型y坐标值,也就是虚部,它必须和参数1具有相同的大小(size值的大小,不是value值的大小)。
函数cv2.magnitude()的返回值是参数1和参数2的平方和的平方根,公式为:
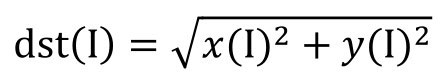
式中,I表示原始图像,dst表示目标图像。
得到频谱信息的幅度后,通常还要对幅度值做进一步的转换,以便将频谱信息以图像的形式展示出来。简单来说,就是需要将幅度值映射到灰度图像的灰度空间[0,255]内,使其以灰度图像的形式显示出来。
result = 20*np.log(cv2.magnitude(实部,虚部))
下面对一幅图像进行傅里叶变换,帮助读者观察上述处理过程。如下代码针对图像“lena”进行傅里叶变换,并且计算了幅度值,对幅度值进行了规范化处理:
import numpy as np
import cv2
img = cv2.imread('image\\lena.bmp',0)
# 傅里叶变换
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
print(dft)
# 移到中间
dftShift = np.fft.fftshift(dft)
print(dftShift)
# 计算频谱信息幅度
result = 20*np.log(cv2.magnitude(dftShift[:, :,0], dftShift[:, :,1]))
print(result)
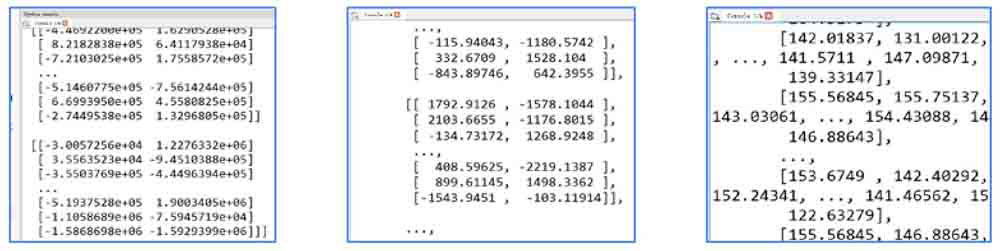
- 左图显示的是函数cv2.dft()得到的频谱值,该值是由实部和虚部构成的。
- 中间的图显示的是函数cv2.magnitude()计算得到的频谱幅度值,这些值不在标准的图像灰度空间[0, 255]内。
- 右图显示的是对函数cv2.magnitude()计算得到的频谱幅度值进一步规范的结果,现在值的范围在[0, 255]内。
实例四:用OpenCV函数对图像进行傅里叶变换,并展示其频谱信息
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('image\\lena.bmp',0)
# 傅里叶变换
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
# 零频域移动中间
dftShift = np.fft.fftshift(dft)
# 得到频谱范围结果
result = 20*np.log(cv2.magnitude(dftShift[:, :,0], dftShift[:, :,1]))
# 显示图像
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122), plt.imshow(result, cmap = 'gray')
plt.title('result'), plt.axis('off')
plt.show()

# 2.实现逆傅里叶变换
在OpenCV中,使用函数cv2.idft()实现逆傅里叶变换,该函数是傅里叶变换函数cv2.dft()的逆函数。其语法格式为:
返回结果=cv2.idft(原始数据)
对图像进行傅里叶变换后,通常会将零频率分量移至频谱图像的中心位置。如果使用函数numpy.fft.fftshift()移动了零频率分量,那么在进行逆傅里叶变换前,要使用函数numpy.fft.ifftshift()将零频率分量恢复到原来位置。
在进行逆傅里叶变换后,得到的值仍旧是复数,需要使用函数cv2.magnitude()计算其幅度。
实例五:用OpenCV函数对图像进行傅里叶变换、逆傅里叶变换,并展示原始图像及经过逆傅里叶变换后得到的图像。
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('image\\lena.bmp',0)
# 傅里叶变换
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
# 零点移动到中间
dftShift = np.fft.fftshift(dft)
# 零点还原
ishift = np.fft.ifftshift(dftShift)
# 逆傅里叶变换
iImg = cv2.idft(ishift)
# 计算幅度
iImg= cv2.magnitude(iImg[:, :,0], iImg[:, :,1])
# 显示图像
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122), plt.imshow(iImg, cmap = 'gray')
plt.title('inverse'), plt.axis('off')
plt.show()

# 3.低通滤波示例
将傅里叶变换结果图像result中的高频信号值都替换为0(处理为黑色),就屏蔽了高频信号,只保留低频信号,从而实现了低通滤波。

在实现低通滤波时,可以专门构造一个如图左图所示的图像,用它与原图的傅里叶变换频谱图像进行与运算,就能将频谱图像中的高频信号过滤掉。

可以采用如下方式构造:
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
# 将所有点填充黑色
mask = np.zeros((rows, cols,2), np.uint8)
# 将中心填充白色构成左1图
mask[crow-30:crow+30, ccol-30:ccol+30] = 1
然后,将其与频谱图进行运算,实现低通滤波。
fShift = dftShift*mask
实例六:使用函数cv2.dft()对图像进行傅里叶变换,得到其频谱图像。然后,在频域内将其高频分量的值处理为0,实现低通滤波。最后,对图像进行逆傅里叶变换,得到恢复的原始图像。观察傅里叶变换前后图像的差异。
import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('image\\lena.bmp',0)
# 傅里叶变换
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
# 移动到中间
dftShift = np.fft.fftshift(dft)
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
mask = np.zeros((rows, cols,2), np.uint8)
#两个通道,与频域图像匹配
mask[crow-30:crow+30, ccol-30:ccol+30] = 1
# 构建低频滤波
fShift = dftShift*mask
ishift = np.fft.ifftshift(fShift)
iImg = cv2.idft(ishift)
iImg= cv2.magnitude(iImg[:, :,0], iImg[:, :,1])
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('original'), plt.axis('off')
plt.subplot(122), plt.imshow(iImg, cmap = 'gray')
plt.title('inverse'), plt.axis('off')
plt.show()
